以前本ブログで扱った、電磁誘導と誘導起電力についての例題を、今度は導線内の自由電子に働くローレンツ力に注目して考えてみます。
今、一様な磁場 $\Bs{B}$ がある。
長さ $\ell$ の導線をその一方を中心にして、図のように磁場を垂直に横切るように角速度 $\omega$ で回転させたとき、導線に生じる誘導起電力の向きと大きさを答えよ。
ただし、導線内の自由電子に働くローレンツ力から求めよ。

ここからは、上から見た次の図を使って考えることにします。
ただし、導線の運動が描く円軌道の中心を $\text{O}$ として、導線 $\text{O}\text{P}$ は時間 $\Delta t$ の間に $\text{O}\text{P}’$ の位置まで動くものとします。

![]() は画面手前から奥に向かう方向、
は画面手前から奥に向かう方向、![]() は画面奥から手前に向かう方向を表す記号です。
は画面奥から手前に向かう方向を表す記号です。
これらは、ネジの頭の穴と先端の尖った部分をイメージして使われています。
ここまでは前回と同じですが、ここからは新たに導線内部の自由電子が受けるローレンツ力に注目してみます。
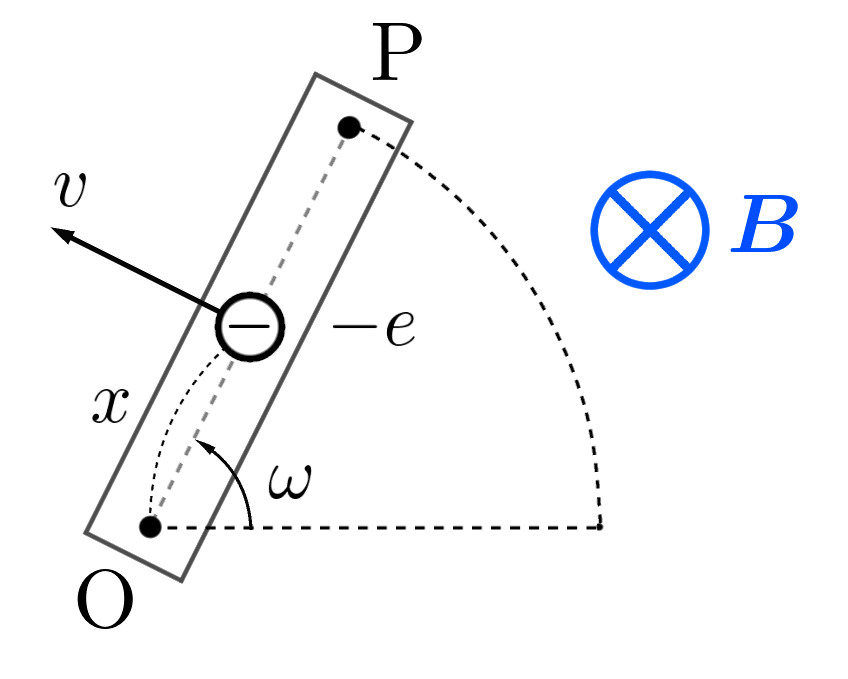
①導線と共に動く自由電子に働くローレンツ力
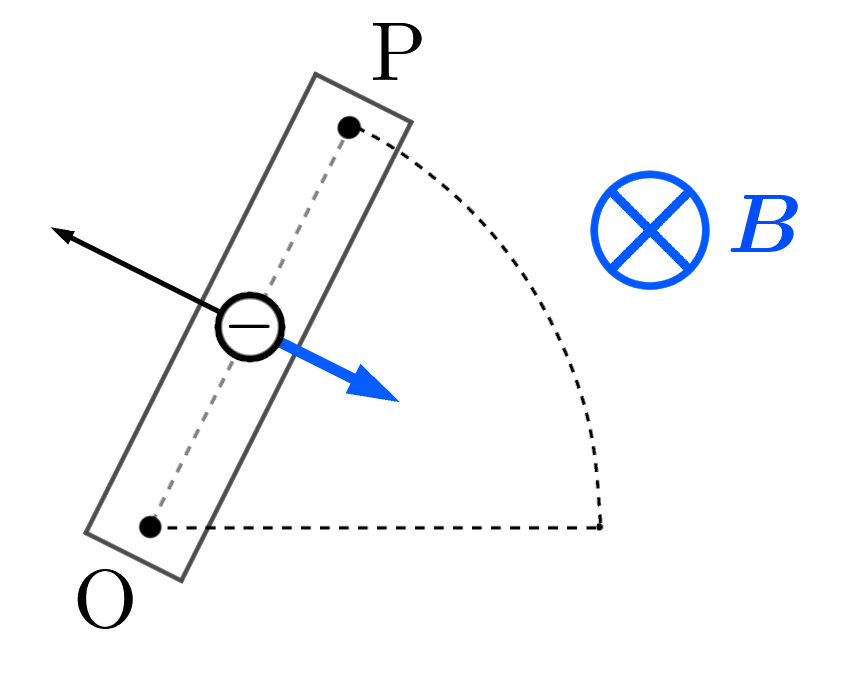
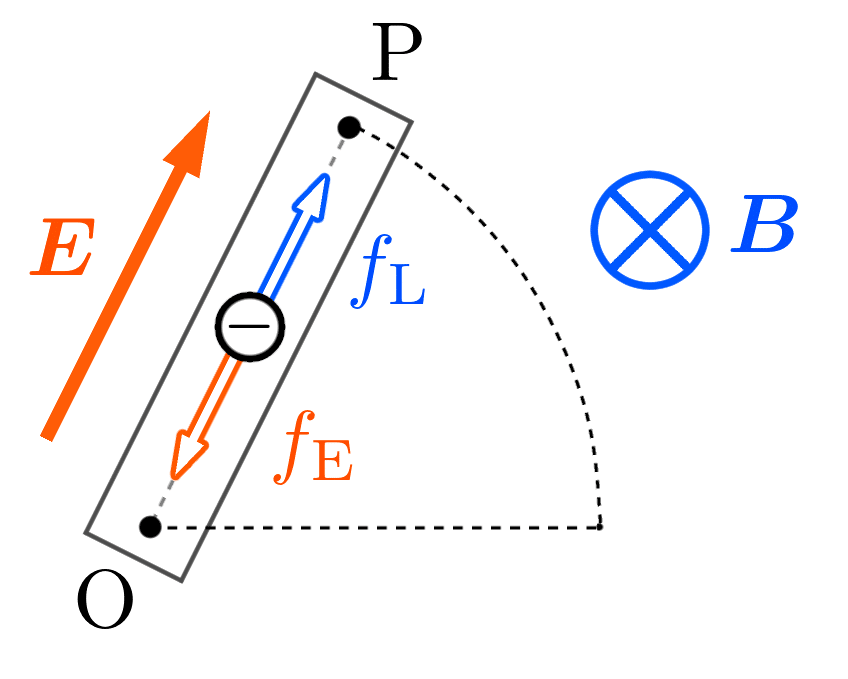
まず、導線といっしょに動く自由電子によって、上図の青色矢印の向きに電流が流れます。
(電流が流れる向きは、負の電荷の自由電子が動いた方向とは逆向きですよね。)
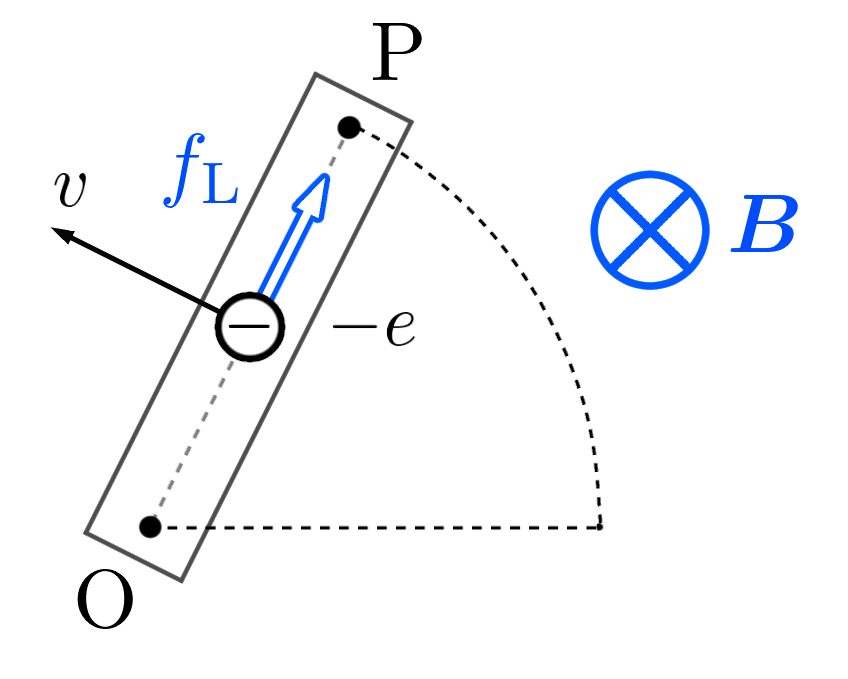
そして、流れた電流と元からある磁場によって、ローレンツの法則から自由電子には上図のような向きに、大きさ $f_\text{L}$ のローレンツ力が働きます。
ローレンツ力の大きさを計算するために、自由電子の速さ $v=x\omega$ を使います。
\begin{align}
f_\text{L}=\abs{-e}vB=ex\omega B\,.\label{fL}
\end{align}
次に、このようなローレンツ力によって生じる変化を見ていきます。
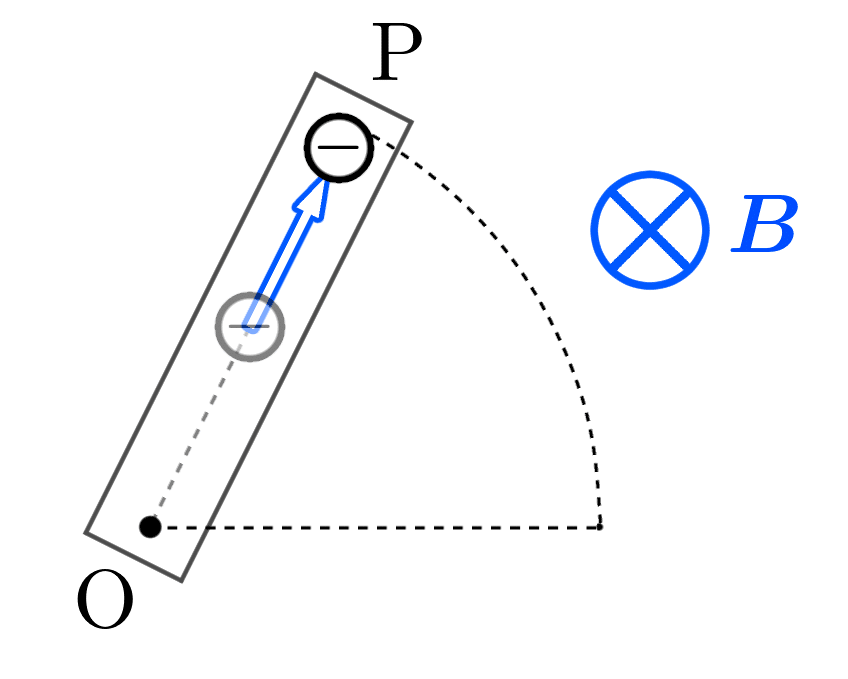
ローレンツ力によって、自由電子は導線の端の点 $\text{P}$ に移動します。
これにより、点 $\text{P}$ の側はマイナスに帯電します。
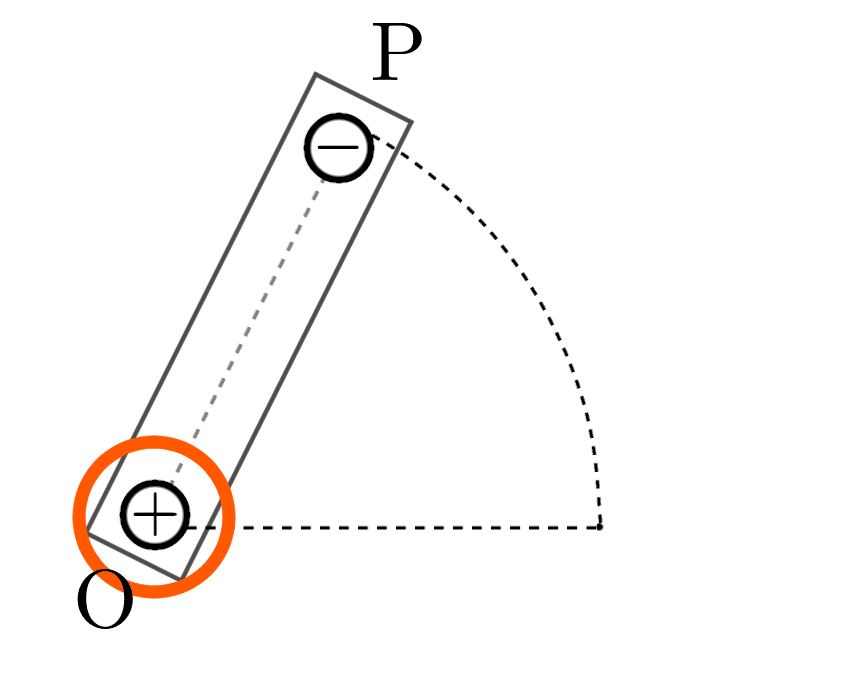
すると、その逆側の端である点 $\text{O}$ は、プラスに帯電します。
このことによって、導線内部にどのような変化が生じるのでしょうか?
次にそれを見ていきます。
②発生した誘導電場によって自由電子に働く力
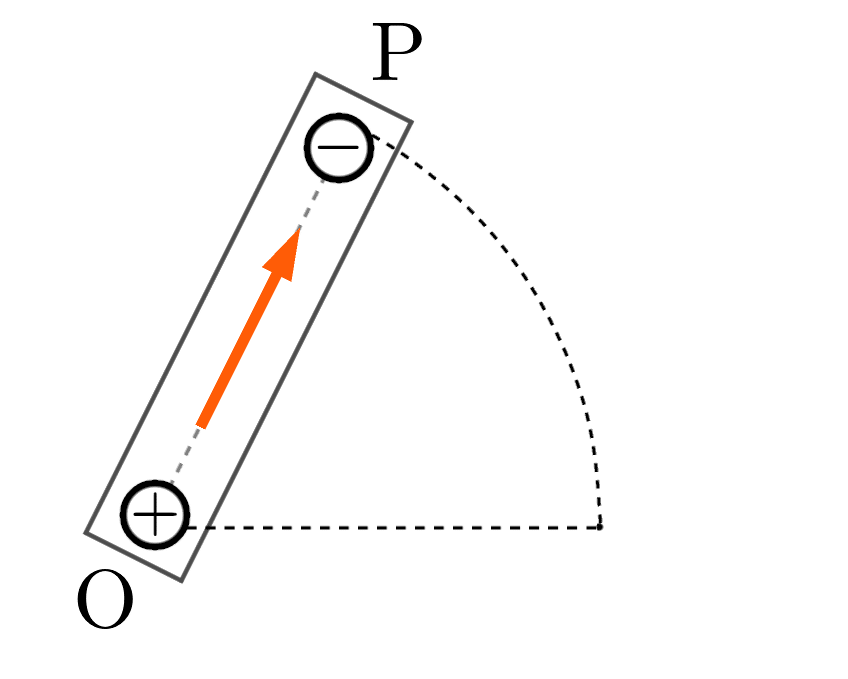
まず、点 $\text{O}$ から点 $\text{P}$ に向かって、電流が流れます。
これは、点 $\text{O}$ の側がプラスに帯電、点 $\text{P}$ の側がマイナスに帯電しているせいで、点 $\text{O}$ の側の方が高電位であることからわかります。
また、電流が流れるということは、導線内部には次図のような向きの電場 $\Bs{E}$ が発生しています。
(このような電場のことを、誘導電場と呼ぶこともあります。)
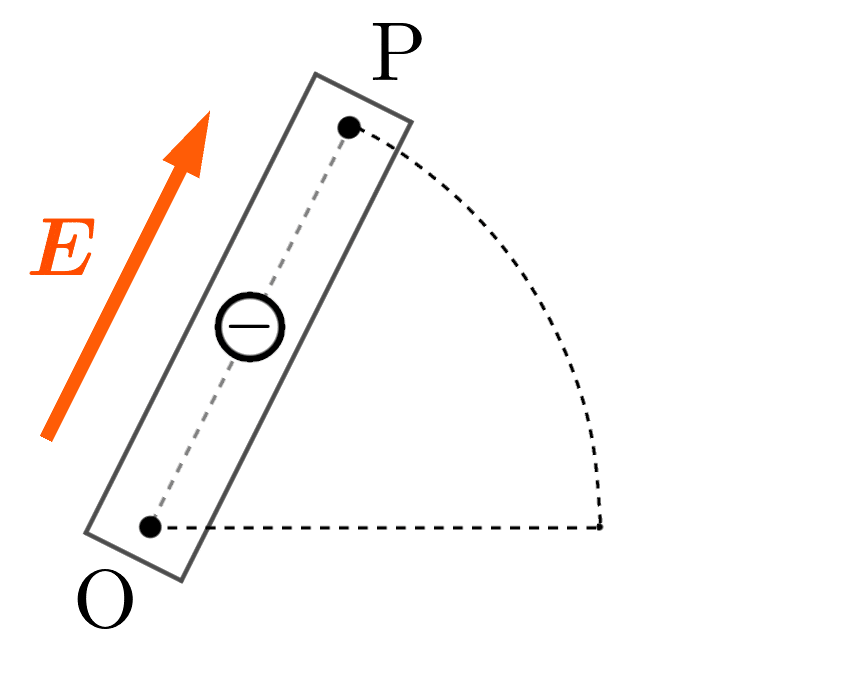
誘導電場によって、負の電荷 $-e$ を持つ自由電子には次図のような向きに力 $f_\text{E}$ が働きます。
力の向きに注意してください。
先程も書きましたが、電流の流れる向きとは逆向きに電子は動きます。
また、電場が電荷 $q$ に及ぼす力は $\Bs{f}=q \Bs{E}$ と表されますが、この式は正電荷について記述しています。
負の電荷 $-q$ を持つ電子に及ぼす力は $\Bs{f}=-q \Bs{E}$ であり、電場 $\Bs{E}$ とは逆向きです。
このように、ベクトルで考えた方がわかりやすいと思います。
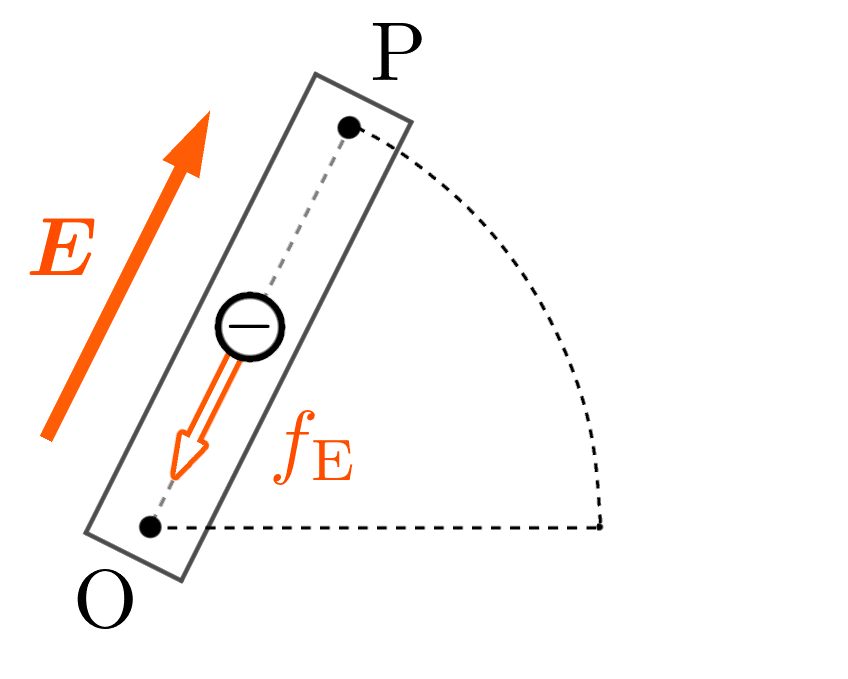
自由電子が誘導電場から受ける力の大きさは、次のように計算できます。
\begin{align}
f_\text{E}=\abs{-e}E=eE\,.\label{fE}
\end{align}
①と②の力のつり合いから起電力を求める
これまで見てきた①と②の力によって、導線内部の自由電子はどのような振る舞いをするのか、改めて振り返ってみましょう。
まず、①の力が生じたことで、導線の両側は逆符号の電荷に分かれ、電位差が生じました。
このような動きがもっと進んだと仮定すると、電位差はどんどん大きくなっていくはずです。
しかし、誘導電場が発生して②の力が生じたことで、電位差の増大は抑制され、その値はどこかで落ち着きます。
このような状態では、導線内部の自由電子は平均的に見てつり合いがとれた状態になっているはずです。
力のつり合いがとれていない場合には、自由電子は加速度を持った運動をしますが、それだと自由電子の持つエネルギーは常に変化するはずです。
しかし、そのようなことは起きていないため、自由電子は等速度運動をしていると考えます。
すみません。ここの説明は良くないです。
十分に理解できていないことを書いているのでご注意ください。
\eqref{fL}と\eqref{fE}の力のつり合いから、電場の大きさが求められます。
\begin{align*}
ex\omega B&=eE\,,\\
\therefore \, E(x)&=x\omega B\,.
\end{align*}
このことから、導線 $\text{OP}$ 上で $E(x)$ を $x$ について積分すると、電位差 $V$ が求められます。
\begin{align*}
V&=\int_{0}^{\ell}E(x)dx\\
&=\int_{0}^{\ell}(x\omega B)dx\\
&=\dfrac{1}{2}\omega B\ell^2\,.
\end{align*}





コメント